Урок
5: Свет
Как вы помните, в четвертом уроке мы сделали большой шаг вперед, и наконец-то окончательно отошли от плоских фигур. Модель была объемной и она вращалась, но все равно оставалась какой-то "недоделанной". В чем причина?
Как известно, мы воспринимаем окружающий мир во многом благодаря нашему зрению. Свет, отражаясь от множества предметов и вещей, попадает на сетчатку наших глаз и создает в голове реальную картину окружающего нас мира. Если бы не было света, то мы бы просто ничего не увидели. И это есть ответ на наш вопрос. Нам не хватает в нашей программе света.
Свет состоит из мельчайших сгустков энергии (частиц), называемых фотонами. Фотон, с одной стороны, это частица, с другой стороны - волна, это означает, что он имеет свойства, присущие как волнам, так и частицам. Эти энергетические сгустки отрываются от источника энергии и прямолинейно распространяются в пространстве, пока не произойдет столкновение с каким-нибудь внешним объектом. Фотонов очень много. Так много, что мы можем сказать - их неопределенно много. Исходя из этого, мы можем пренебречь фактом, что свет состоит из единичных фотонов и рассмотреть свет как непрерывный поток энергии. В этом случае к свету можно применить статистические законы, и полученные результаты будут достаточно аккуратны именно благодаря огромному количеству вовлеченных фотонов. Таким образом, свет может быть легко нами смоделирован.
Очень важно знать, как много света будет в любой точке на поверхности нашего объекта.

Когда поверхность целиком обращена к свету - максимальное количество света достигает ее. Вся поверхность освещена.
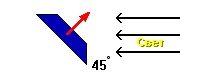
Когда поверхность расположена под некоторым углом к падающему на нее свету, площадь сечения, обращенного к свету, становится меньше. Что выражается в меньшем количестве световой энергии, воздействующей на поверхность.

Когда вектор нормали (Нормаль - это вектор, перпендикулярно направленный по отношению к плоскости поверхности) к плоскости поверхности находится под прямым углом к падающему свету, то свет просто-напросто проходит мимо поверхности, и она совсем не освещается. Таким образом, количество световой энергии, воздействующей на поверхность, есть функция от ориентации поверхности по отношению к воздействующим лучам света. Исходя из этого, мы можем найти значение отраженного света от поверхности.
отраженный свет = clamp(N dot L)*С
,где
N - вектор нормали
L - вектор
источника света
С - цвет
поверхности
dot -
скалярное произведение двух векторов
clamp()
- функция, отсекающая отрицательные значения
Скалярным произведением векторов нормали и источника света мы найдем степень освещенности поверхности, а умножая ее на цвет поверхности, получаем значение отраженного света.
Теперь сделаем некоторые изменения в нашей программе. Во-первых, необходимо занести новые значения в константные регистры вершинного шейдера.
//
Функция SetVertexShaderConstants() устанавливает
// значения константных регистров вершинного шейдера
void SetVertexShaderConstants(void)
{
D3DXCOLOR d3dx_diffuse_color(0.3f,0.7f,0.7f,0.0f);
D3DXVECTOR4 d3dx_light_vector(0.0f,0.0f,-1.0f,0.0f);
D3DXVECTOR4 d3dx_constants(0.0f,1.0f,0.0f,0.0f);
// Устанавливаем константу цвета модели в регистр c12
d3d_device->SetVertexShaderConstant(12,&d3dx_diffuse_color,1);
// Устанавливаем константу вектора источника света в
регистр c13
d3d_device->SetVertexShaderConstant(13,&d3dx_light_vector,1);
// Устанавливаем константу в регистр c14
d3d_device->SetVertexShaderConstant(14,&d3dx_constants,1);
}
Во-вторых, изменится фунция установки матриц.
//
Функция SetMatrices() устанавливает матрицы преобразований
void SetMatrices(void)
{
D3DXMATRIX d3dx_matrix_world;
D3DXMATRIX d3dx_matrix_view;
D3DXMATRIX d3dx_matrix_world_view;
D3DXMATRIX d3dx_matrix_proj;
D3DXMATRIX d3dx_matrix1,d3dx_matrix2;
// Расчет мировой матрицы
D3DXMatrixRotationX(&d3dx_matrix1,timeGetTime()/1000.0f);
D3DXMatrixRotationY(&d3dx_matrix2,timeGetTime()/500.0f);
D3DXMatrixMultiply(&d3dx_matrix_world,&d3dx_matrix1,&d3dx_matrix2);
// Расчет видовой матрицы
D3DXMatrixLookAtLH(&d3dx_matrix_view,&D3DXVECTOR3(0.0f,0.0f,-30.0f),
&D3DXVECTOR3(0.0f,0.0f,0.0f),
&D3DXVECTOR3(0.0f,1.0f,0.0f));
// Расчет мировой и видовой матрицы
D3DXMatrixMultiply(&d3dx_matrix_world_view,&d3dx_matrix_world,&d3dx_matrix_view);
// Расчет проектной матрицы
D3DXMatrixPerspectiveFovLH(&d3dx_matrix_proj,D3DX_PI/4,1.0f,1.0f,100.0f);
// Заносим матрицы в вершинный шейдер
D3DXMatrixTranspose(&d3dx_matrix1,&d3dx_matrix_world);
d3d_device->SetVertexShaderConstant(0,&d3dx_matrix1,4);
D3DXMatrixTranspose(&d3dx_matrix1,&d3dx_matrix_world_view);
d3d_device->SetVertexShaderConstant(4,&d3dx_matrix1,4);
D3DXMatrixTranspose(&d3dx_matrix1,&d3dx_matrix_proj);
d3d_device->SetVertexShaderConstant(8,&d3dx_matrix1,4);
}
Как видите, я совместил мировую и видовую матрицу в одну d3dx_matrix_world_view, чтобы сократить количество вычислений в вершинном шейдере. Теперь рассмотрим его работу.
;------------------------------------------------------------------------------
; Vertex transformation
;------------------------------------------------------------------------------
; Transform to world space and to view space
m4x4 r0, v0, c4
; Transform to projection space
m4x4 r0, r0, c8
;------------------------------------------------------------------------------
; Normal transformation
;------------------------------------------------------------------------------
; Transform to world space
m4x4 r1, v3, c0
Сперва, как обычно происходит трансформация позиции вершины. К ней добавилась трансформация нормали в мировые координаты.
;------------------------------------------------------------------------------
; Lighting calculation
;------------------------------------------------------------------------------
dp3 r2.x, r1, c13
max r2.x, r2.x, c14.x
mul r3, r2.x, c12
; Store output position
mov oPos, r0
; Store output color
mov oD0, r3
Преобразованный вектор нормали мы скалярно умножаем на вектор света, который хранится в регистре c13. Отрицательные значения отсекаем командой max, и полученную степень освещенности, умножаем на цвет вершины.

Рисунок 1. Модель космического корабля
В итоге мы получили еще более красивую модель космического корабля. Исходный текст этой программы и exe-файл вы можете взять здесь. Не забудьте, взять файл с моделью корабля в архиве из предыдущего урока.